前ページに示しましたように,”母分散σがわかっている場合”の区間推定の計算方法を示しました.
\(\Large \bar{x} - 1.96 \times \sqrt{\frac{\sigma^2}{n}} \hspace{12 pt}\leq \hspace{12 pt} \mu \hspace{12 pt} \leq \hspace{12 pt} \bar{x} + 1.96 \times \sqrt{\frac{\sigma^2}{n}} \)
すなわち,
測定平均,\(\Large \bar{x} \) と母分散σ2,と試行回数nがわかれば,母平均μの範囲がわかる=区間推定ができる
というものでした.
しかし,そもそもわからないものを推定するのですから,母分散σ2,だってわからないのが当然でしょう.
測定からわかるのはせいぜい,不偏分散,ぐらい...
\(\Large \displaystyle s^2 = \frac{ \displaystyle \sum_{i=1}^n (x_i - \bar{x})^2}{n-1} \)
じゃあ,何とか,σ2とsが入った関係式を見つけ出し,それをうまく組み合わせることにより,σ2を消去し,sを残せば,実際に得られたデータから区間推定ができるんじゃないかと考えたのが,
t検定
です(と思います.....).
つまり,母分散がわかっている状態での区間推定で使われている指標をZとすると,
\(\Large Z =\displaystyle \frac{\bar{x} - \mu}{ \sqrt{\frac{\sigma^2}{n}}} \rightarrow \frac{\bar{x} - \mu}{ \sqrt{\frac{s^2}{n}}} = t \)
と変換すればいいのです.これからの導出は,こちらのサイト,を参考にしました,ありがとうございます.まず,
\(\Large \displaystyle s^2 = \frac{ \displaystyle \sum_{i=1}^n (x_i - \bar{x})^2}{n-1} \)
です,すると,
\(\Large t = \displaystyle \frac{\bar{x} - \mu}{ \sqrt{\frac{s^2}{n}}} = \frac{\bar{x} - \mu}{ \sqrt{ \displaystyle \frac{1}{n} \displaystyle \frac{ \displaystyle \sum_{i=1}^n (x_i - \bar{x})^2}{n-1}}}\)
となります.
ここで,新しい指標,U,を導入します.ここには,σ2とsが入っているので期待大です
\(\Large \displaystyle U = \frac{(n-1) s^2}{ \sigma^2} = \frac{ \displaystyle \sum_{i=1}^n (x_i - \bar{x})^2}{ \sigma^2} = \chi_{n-1}^2\)
最後の,
\(\Large \displaystyle \chi_{n-1}^2\)
は自由度1のカイ二乗分布となります(導出はこちらで)
\(\Large \displaystyle s^2 = \frac{ U \sigma^2}{ n-1} \)
となるので,
\(\Large \displaystyle Z =\displaystyle \frac{\bar{x} - \mu}{ \sqrt{\frac{\sigma^2}{n}}} \rightarrow \bar{x} - \mu = \sqrt{ \frac{\sigma^2}{n}} Z\)
\(\Large \displaystyle t = \frac{\bar{x} - \mu}{ \sqrt{\frac{s^2}{n}}} \rightarrow \frac{\sqrt{ \frac{\sigma^2}{n}} Z}{ \sqrt{\frac{s^2}{n}}}
=
\displaystyle \frac{\sqrt{ \frac{\sigma^2}{n}} Z}{ \displaystyle \sqrt{\frac{1}{n} \frac{U \sigma^2}{n-1}}}
= \frac{Z}{\sqrt{ \frac{U}{n-1}}}
\)
とtの分布は,自由度n-1のカイ二乗分布(U)とZ(標準化正規分布)に従う分布となります.
実際のtの値は,
\(\Large \displaystyle t = \frac{\sqrt{ \frac{\sigma^2}{n}} Z}{ \sqrt{\frac{s^2}{n}}} \)
ですが,
\(\Large Z =\displaystyle \frac{\bar{x} - \mu}{ \sqrt{\frac{\sigma^2}{n}}} \)
ですので,
\(\Large \displaystyle t = \frac{\sqrt{ \frac{\sigma^2}{n}} Z}{ \sqrt{\frac{s^2}{n}}} = \frac{\bar{x} - \mu}{ \sqrt{\frac{s^2}{n}}}\)
として実験結果から計算することができます.
つまり,
母分散がわかっている場合は,
\(\Large \displaystyle - 1.96 \hspace{52 pt}\leq \hspace{12 pt} \frac{\mu - \bar{x}}{ \sqrt{\frac{\color{red}{\sigma}^2}{n}}} \hspace{12 pt} \leq \hspace{12 pt} 1.96 \)
母分散がわからない場合には,
\(\Large \displaystyle - t_{\alpha/2} (n-1) \hspace{12 pt}\leq \hspace{12 pt} \frac{\mu - \bar{x}}{ \sqrt{\frac{\color{red}{s}^2}{n}}} \hspace{12 pt} \leq \hspace{12 pt} t_{\alpha/2} (n-1) \)
となるのです.
t分布自体は,
\(\Large \displaystyle f(t) = \frac{ \Gamma (\frac{n}{2}) }{ \sqrt{(n-1) \pi} \ \Gamma ( \frac{n-1}{2})} \left( 1 + \frac{t^2}{n-1} \right)^{- \frac{n}{2}}\)
となりますが,この導出は.....ここ,にありますが...勉強します.
なんとか解けました!,ここ,に記しました!
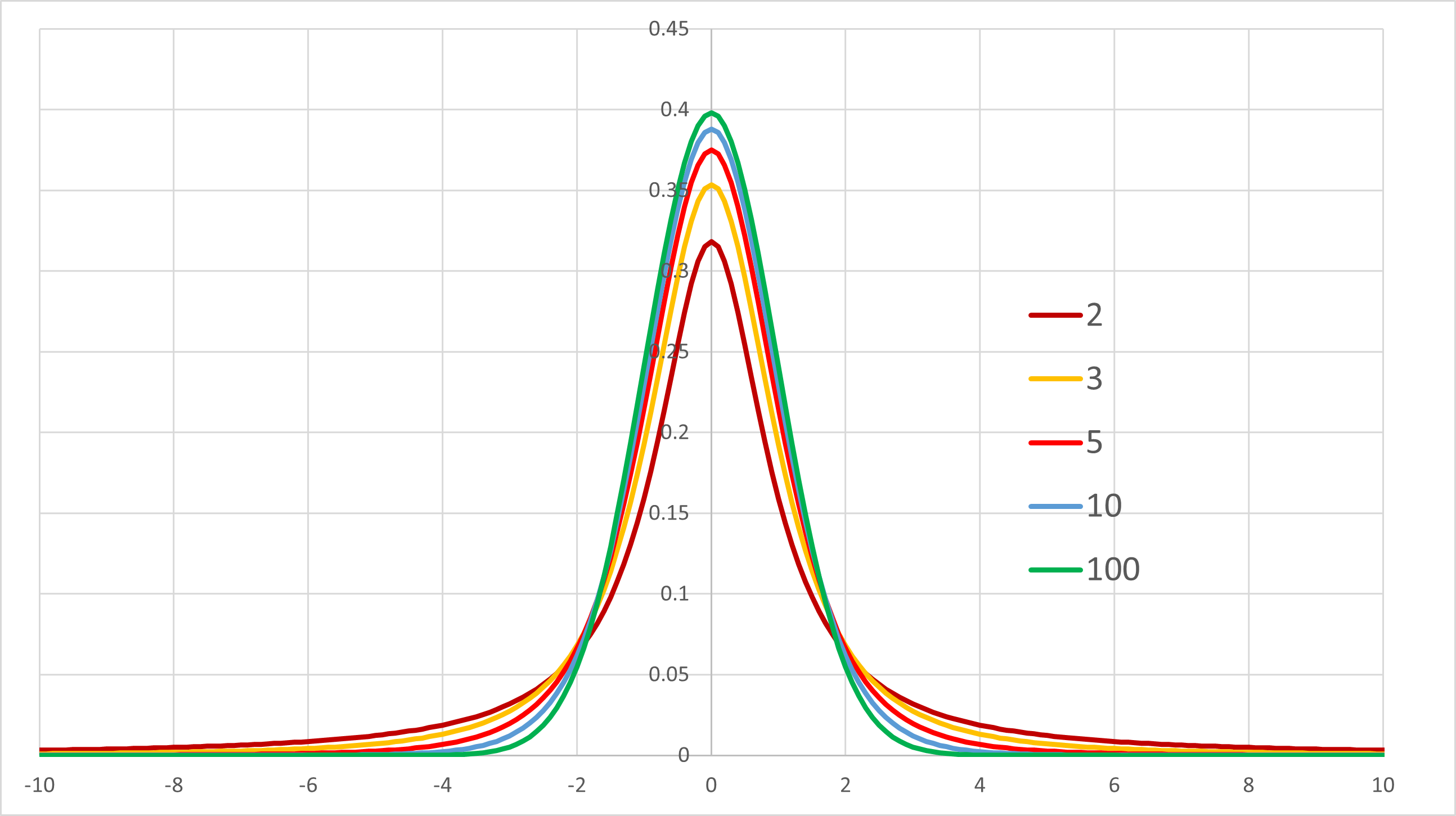
実際の波形は,

と若干先鋭化した正規分布のような形となります.
では,ここで重要となる,
\(\Large \displaystyle \chi_{n-1}^2 \)
という,自由度1のカイ二乗分布を検討していきましょう.